The Basics of Multiple Regression Analysis: A Step-by-Step Guide
Multiple regression analysis is one of the most fundamental and widely used techniques in econometrics and data analysis. It is primarily used to understand the relationship between one dependent variable and two or more independent variables. This method allows researchers to isolate the effect of each independent variable while controlling for the effects of others. In this article, we will break down the basics of multiple regression analysis, guide you through the essential concepts, and provide a step-by-step approach to conducting and interpreting the analysis.
What is Multiple Regression?
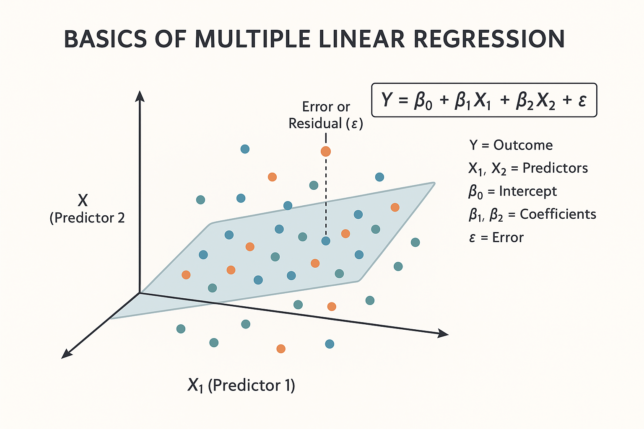
Multiple regression is a statistical technique that models the relationship between a dependent variable and two or more independent variables. The general form of a multiple regression equation is: Y=β0+β1X1+β2X2+…+βkXk+ϵY = \beta_0 + \beta_1X_1 + \beta_2X_2 + … + \beta_kX_k + \epsilon
Where:
- YY is the dependent variable (the outcome you’re trying to predict),
- X1,X2,…,XkX_1, X_2, …, X_k are the independent variables (the predictors or factors affecting YY),
- β0\beta_0 is the intercept (the value of YY when all XX variables are zero),
- β1,β2,…,βk\beta_1, \beta_2, …, \beta_k are the coefficients that represent the effect of each independent variable on the dependent variable,
- ϵ\epsilon is the error term (the part of YY that cannot be explained by the model).
Multiple regression analysis allows us to estimate the relationship between several independent variables and a dependent variable simultaneously, making it particularly useful for complex economic, social, and scientific models.
Assumptions of Multiple Regression
Before diving into the analysis, it’s important to understand the assumptions that underlie multiple regression. These assumptions must be satisfied to ensure the validity of the results:
- Linearity: There is a linear relationship between the dependent variable and the independent variables. This means that the effect of an independent variable on the dependent variable is constant across all values of the independent variable.
- No Multicollinearity: The independent variables should not be highly correlated with each other. If they are, it can be difficult to separate their individual effects on the dependent variable.
- Homoscedasticity: The variance of the errors (ϵ\epsilon) should be constant across all levels of the independent variables. In other words, the spread of the residuals should be the same for all predicted values of YY.
- Independence of Errors: The errors (ϵ\epsilon) should be independent of each other, meaning that the value of one residual should not provide information about another residual.
- Normality of Errors: The errors should be normally distributed. This assumption is important for hypothesis testing and confidence intervals.
Step-by-Step Guide to Performing Multiple Regression
Step 1: Define Your Research Question
The first step in performing a multiple regression analysis is to clearly define your research question. For instance, you might want to predict the sales of a product based on factors such as advertising budget, price, and customer satisfaction. Your dependent variable (sales) is being influenced by three independent variables: advertising budget, price, and customer satisfaction.
Step 2: Collect the Data
Next, you need to collect data for both the dependent and independent variables. This could come from surveys, experiments, or publicly available datasets. For the regression model to be meaningful, ensure that the data is reliable, accurate, and contains enough variation to capture the relationships you’re interested in.
For example, you might gather data for the following variables:
- Y (Dependent Variable): Sales (in units)
- X1 (Independent Variable): Advertising budget (in dollars)
- X2 (Independent Variable): Price (in dollars)
- X3 (Independent Variable): Customer satisfaction (on a scale from 1 to 10)
Step 3: Check the Assumptions
Before running the regression, it’s crucial to check whether the assumptions of multiple regression are met. For example:
- Linearity can be checked by plotting scatterplots of each independent variable against the dependent variable. A linear pattern should emerge.
- Multicollinearity can be tested using the Variance Inflation Factor (VIF). VIF values above 10 suggest problematic multicollinearity.
- Homoscedasticity can be checked by plotting the residuals against the fitted values (predicted values of YY) and ensuring the spread remains constant.
- Independence of errors can be tested using the Durbin-Watson statistic, which should be close to 2.
- Normality of errors can be tested using a histogram or Q-Q plot of the residuals. A bell-shaped curve indicates normality.
Step 4: Run the Multiple Regression
Once you have your data and have confirmed the assumptions, you can run the regression analysis. In R, Python, or other statistical software, this can be done using built-in functions. Here is how you might run a multiple regression in R:
model <- lm(Y ~ X1 + X2 + X3, data = your_data)
summary(model)In Python (using statsmodels), it would look like this:
import statsmodels.api as sm
X = data[['X1', 'X2', 'X3']] # Independent variables
X = sm.add_constant(X) # Adds intercept to the model
y = data['Y'] # Dependent variable
model = sm.OLS(y, X).fit()
print(model.summary())
Step 5: Interpret the Results
The output of a multiple regression analysis typically includes the coefficients, p-values, R-squared, and other statistics.
- Coefficients: These tell you the effect of each independent variable on the dependent variable. For example, if the coefficient of X1X_1 (advertising budget) is 2, this means that for each additional dollar spent on advertising, sales increase by 2 units, assuming all other variables remain constant.
- P-values: These help you determine whether each independent variable is statistically significant. A p-value below 0.05 generally indicates that the variable is statistically significant.
- R-squared: This statistic measures how well the independent variables explain the variation in the dependent variable. An R-squared value closer to 1 indicates a better fit of the model.
- Adjusted R-squared: This is a modified version of R-squared that adjusts for the number of independent variables in the model. It’s especially useful when comparing models with different numbers of predictors.
- Standard Errors: These indicate the variability of the coefficient estimates. Smaller standard errors imply more precise estimates.
Step 6: Make Predictions
Once the model is fitted, you can use it to make predictions. For instance, given new data on advertising budget, price, and customer satisfaction, you can predict future sales. This is done by plugging the new values into the regression equation.
new_data <- data.frame(X1 = 5000, X2 = 20, X3 = 8)
predict(model, new_data)
Step 7: Validate the Model
Finally, it’s important to validate your regression model. This can be done by:
- Cross-validation: Splitting your data into training and testing sets to see how well the model generalizes to new data.
- Residual analysis: Examining the residuals (the differences between predicted and actual values) to ensure that the assumptions hold.
Conclusion
Multiple regression is a powerful tool for understanding complex relationships between variables and predicting outcomes based on multiple factors. By following the steps outlined in this guide, you can apply multiple regression analysis to a variety of research questions and datasets. However, always ensure that the assumptions are met, and validate your model to ensure its robustness. With practice, multiple regression will become an indispensable tool in your econometrics toolkit, helping you analyze data and make informed decisions based on evidence.